We shall begin by explaining in a little more detail the main reasons for all the experiments you have seen in the previous post.
One of the most important reasons behind those experiments was to introduce you to what I'll show to be perhaps the most obvious error in the conventional understanding of the prismatic phenomena. The error I'm referring to is summarised in the screenshot below, which I took from here.
status:all
It is truly incredible that the conventional understanding can be so wrong in such a simple and obvious matter. And it is even he best way of explaining why it is wrong. That's because there are so many things wrong in the conventional explanation that I simply don't know where to begin. Fourteen or fifteen years ago, when I first wrote about more incredible how easy it is to prove it. I must tell you that every time I encounter an issue like this (and believe me, there have been many times like this) I find it pretty much impossible to find t this issue, I conducted a very simple experiment to show that the conventional understanding is wrong. See below.
To give a quick explanation of what the three pictures show (if it's really necessary...) I drew a line that divided in two equal halves one face of an equilateral prism. I placed the eye of the observer (camera) at the same level with that line. I then turned around the prism so that the opposite face of the prism was fronting the camera. Lastly, I observed that the line I had drawn exactly halfway across the first face of the prism appeared to have been deflected towards the apex of the prism, even though I had not moved the eye of the observer at all from its original spot.
(A cautionary note. Do not be tempted to argue that my line was drawn right on the face of the prism, instead of being at some distance away from it. It is a silly argument. No, let me rephrase that: It is a stupid argument. Think about it, if you have to.)
To my mind, the simplest way to see that the conventional understanding is flawed is to just grab a prism (preferably a wedge like in the conventional diagram) and look through it at the world around. I believe that if one pays attention at the images observed, and at the prism's location relative to the positions of the objects under observation, it is virtually impossible not to see how wrong the conventional view is. For instance, no observer ever lowers his eye to see an object. He lifts instead the prism to let the object come into the field of vision of his prism. And when that happens more often than not his eye will be pretty much perpendicular to the face of the prism he is looking through. The conventional idea of placing one's eye in the line of refraction is completely irrelevant in subjective observations. Not only that. The sheer reality is that that idea is badly misleading, and that truth is amply manifested in the fact that no one in 350 years has been able to see such simple facts as the following.
Look carefully at the two pictures above. They are images of a wedge prism. To be exact, they are images of half of an equilateral prism. In the first image the tilted face of the prism is fronting the camera. In the second image the flat face of the prism is right in front. Notice the difference between what the first image shows and what is absent from the second.
Now, the question that elicits a definitive answer is this: Why is the base of the prism visible in the first image, but not in the second?
Let me show you another image.
Here we have another prism (a 90⁰/45⁰/45⁰) in which we can see both its base (that appears like an inclined plane) as well as a display of the image of the steel rod appearing to be deviated towards its apex. Both of those things are caused by the same factor, but that factor isn't in any shape or form connected to the conventional understanding. Instead, the real factors that are responsible for the observations we mentioned are deeply connected to the particular field of view each kind of prism basically has. To make our task a little easier have a good look at the illustration below.
In this illustration we have depicted a wedge prism ABC (which essentially is one half of an equilateral prism), its particular field of vision (which is teal coloured) and the seemingly elevated base of this prism EBCD. Now, if one conducts a subjective observation by using this prism, one can only see objects that happen to be located inside the shown field of vision. (This last statement is only in principle true, for the following reasons. A prism is a truly gigantic object, considering the objects it looks at--rays of light. This fact gives the eye of the observer significant liberty to choose its preferred point of observation from amongst the relative many that are possible. For instance, an observer may want to see his object right in the middle of the face of the prism, whilst another may opt for the display to become visible closer to the apex of the prism. You know what I mean? Nonetheless, although the observer has a relatively high degree of freedom in that respect, in reality when a particular position extends the field of view in one direction, at the same time it commensurately reduces it in the direction opposite to it.)
Finally, on this topic, let us explain why the base of the prism is visible in one case but not in the other. This is one of those issues that are dearest to my mind, because I have never seen anyone grasping the fundamental aspect of what a tilted face of a prism really is. Let me begin by reminding you that the human eye (or the eye of a camera, for that matter) is a device that can only see two of the three spatial dimensions. Let's make use of the conventional notation of the spatial axes, with x and y representing the horizontal and the vertical planes, and with z representing the depth of space. The flat reality (pun intended) is that the eye (of either a human or a camera) can only see and record the world around upon a two-dimensional screen. Of course, man has had ample time to find and develop means of fooling his brain into believing that he can see along the z axis as well, but the truth is that the brain can be fooled to such an extent that it 'sees' the depth of space even in a photograph!
This subject seems to be such a difficult issue to grasp that a few years ago, when I said that what a prism does is giving the observer the possibility of seeing along the third dimension of space, a certain Dr. Markus Selmke from Leipzig University told me that he hadn't ever heard anyone talking about the prism like that. I knew that his remark was meant to show me that by saying that I was some kind of a wacko. But the reality was that what I got from that was that physicists are not very smart. They are educated, but almost never smart. In any event, let me show you why I knew that I knew better.
The two pictures shown above are self-explanatory, so the only thing that I will add to what I already said is this: Do you agree with me that I knew better? If you do not, I will change the eye of the camera that is facing the prism with your human eye, and then I will take the prism away and dare you to tell me that you can see what is written on that red strip of paper.
The reason that the base of the prism is visible when the tilted face of the prism is facing the eye of the observer is because the face AC (see the illustration showed earlier above) is partially extending over the z spatial axis. Since the spatial planes are all perpendicular to each other an image of the base BC is projected upon the AC face as if it were extending from C to E, like an inclined plane. On the other hand, when the vertical AB face is fronting the eye of the observer the image of the base BC remains in its original position--lying flat along the z axis.
The last thing that I should mention is that the same reason is responsible for the apparent deviation of an image towards the apex of a prism. And there are even more observational effects that are due to the same reason. For instance, have a good look at the image below and then try to explain the particular distribution of colours in the prism shown by using the same kind of reasoning. Try it, it should be fun.
Another of my claims that is very dear to me is my belief that the spectral colours are distributed longitudinally according to their respective wavelengths (from B to G to R) in a beam of white light. Everybody seems to be astonished by that apparently ostentatious claim, while at the same time I myself am decidedly baffled by their inability to see how profound, parsimonious and beautiful that idea is. Most interestingly, when I discuss this topic with a conventional physicist not one of them is able to offer any argument that carries even a faint smell of plausibility with it. I, on the other hand, can offer you a dozen good reasons why that should be the case.
Before mentioning any of those good reasons let me show you a number of pictures which--to my mind--are clearly revealing a distribution of waves in perfect agreement to my understanding, but which apparently reveal absolutely nothing to the minds of conventional physicists. Here we go.
The image on the left was snapped by a British pilot in the Second World War, right after he had successfully dropped a bomb on a German cruiser. Water basically waves transversally, pretty much like the light does. The image on the right is a diagram I extracted from a paper written by a Chinese physicist, who was at the time the foremost authority in the world on the subject of the observed frequency downshift in the propagation of water waves. That particularly difficult subject came to my attention about fifteen years ago, when I tried to find out if the distribution of water waves was governed by the same set of principles as all other forms of energy propagation, as I believed. It was with a great deal of satisfaction to learn that indeed such was the case in virtually all forms of energy propagation--including in those situations where the propagation of the travelling waves was longitudinally manifested. To my mind that was a no-brainer. Whether some form of energy is travelling from one place to another by waving transversally or longitudinally its spatial distribution (or extension) will display a discreetly quantized formation similar to the spectral VBGYOR orientation. For one quintessential reason: Energy propagation is spatial vibration. Light is spatial vibration. A photon is neither a particle, nor a wave of energy. A photon is a quantum of space which vibrates when it is disturbed by some form of energetic manifestation. A photon does not travel, just like a wave does not travel.
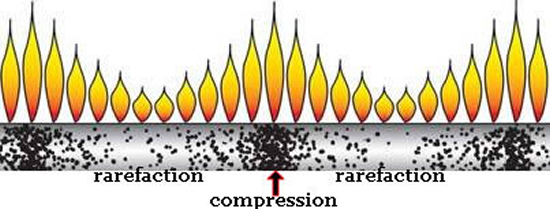
Even a coiled spring will display a kind of 'spectral' distribution, if it is pushed against a wall, for example. An even better display of a longitudinal propagation that shows a similar distribution is routinely witnessed by physics undergraduates. See the picture below.
A steel tube, which is open-ended on both sides is filled with a propane gas. The tube has a series of little holes drilled along the top, and when the lecturer blows air through one end of the tube whilst holding a candle above the tube a series of flames will be ignited by the gas that escapes through those holes. And since air is pushed in a longitudinal direction, the distribution of the gas inside the tube will be compressed at some points and rarefied at others. This situation will therefore create bigger flames in the compression zones and smaller ones in the areas where rarefaction occurs. Now this is supposed to prove that air propagation is longitudinal in nature, but to my mind this proves that even longitudinally there exists a precise distribution of energy which extends in a gradual order from high to low. Just as I said a million times already.
The two pictures above are showing, according to me, how energy is propagating in basically any type of medium. The conventional physicist--alas--has learned nothing from pictures like these. When a conventional physicist talks about how our sun emits light in the form of rays that are basically travelling toward the earth in parallel formations, he obviously has learned nothing from pictures like these. And when he 'explains' that the reason for that idea is because the sun is so big, and the earth is so small!?! And if you ask him what distance is there between two hydrogen atoms that are sitting next to each other (on the sun) and emit one photon each, at the same time, he suddenly begins to panic. And to stutter. And when you ask him to help you draw a dozen parallel lines around a circle, he looks decidedly ready to die. Or to kill you. And it is then when you realise that you just shouldn't try to show him that it is impossible to draw two parallel lines in this Universe.
About two weeks ago someone found necessary to let me know that polarization is proof that light is a transversal wave. Initially I wanted to ignore that comment. Then I was going to reply to it in my typical way of dealing with irrelevant arguments. But then I remembered that many a physicist have thrown at me exactly the same stupidity over the years, so I changed my mind again and quickly concocted a kind of animated picture that I attached to some badly camouflaged bit of politeness in a lifeless reply.
Have a look at the image above. As crude as it may be, it accurately illustrates my understanding of how light propagates in space. The first thing it shows is that in my understanding there are only three spectral colours. BGR are truly sufficient to create any conceivable colour in the entire spectral gamut we know. BGR can also account perfectly for both kinds of prismatic experiments. The second thing the image above shows is that BGR are oscillating transversally to the direction of travel. The only longitudinal thing about BGR is their particular orientation relative to each other. Polarization, therefore, is not a problem at all in my understanding of light. (Besides, it is also worth mentioning here that the newest thing about polarization is that the conventional physics is actually changing its stance in regards to the idea that longitudinal waves cannot be polarized. But that's another story.)
One very important issue about why I believe that the three primary colours are distributed in a BGR pattern in what we call white light is intrinsically linked to the universal morphology of space. Fundamentally, my understanding of light is just like that both Newton and Goethe had. Fundamentally, I believe that light is colourless. It is only when light is confined to the particular geometry of the space it occupies at any given point that it acquires colour, wavelength and frequency.
To see what I mean I have for you five beautiful visual examples that will knock at least some socks off some feet, I'm sure. Those five examples come from here, which is a site of many wonderful scientific applets. In our case the applet we're interested in at the moment is a Fresnel Diffraction Applet. I encourage you wholeheartedly to plan a good visit to this Fresnel diffraction applet, for it is truly fascinating. Go right now and have a quick look first, then click this for the info you need in order to understand what's going on the page with the actual applet, and to make my job a little easier with the presentation of those five examples. In the meantime, I'll drop below the first image and lay down a couple of explanations to make sense of what you'll be looking at.
(I hope you have visited the two links I provided, for then I could rest assured that you have a good chance to grasp the importance of this presentation.)
The image above shows what an observer sees when he looks from his point of observation, which is four metres away from the object under scrutiny--a small hole about 5 mm in diameter drilled in an opaque screen, on which white light is shined. The white light is provided by three RGB lights. The red circle is basically the area over which the effects of diffraction are observed. On the right half of the image there are a few variables that can be adjusted or changed. One of those variables that is of interest to us is the size of the aperture (the hole's diameter). For the image above the size of the hole remained unchanged. To guide us in our journey I placed a red double arrow in the aperture's field. As we'll change the size of the aperture, I will mark each increasement accordingly. That's about all the info that we need for our current purpose.
So, we have a small aperture on which white light is shined and a kind of blueish colour is recorded.
Image number 2. To obtain this image I have increased slightly the diameter of the hole. I have marked this change by placing a red double arrow that extends from one side of the hole to the other. Not much has changed for the observer, except that the blueish colour is more prominent. That was to be expected, since by increasing the aperture more light is coming towards the observer.
Image number 3. We have again increased marginally the size of the aperture, and this time there is a visible change in the colours observed. The blueish colour is now surrounded by a band of reddish hue. Moreover, the reddish band appears to have spread over the boundary of the red circle.
Image number 4. Increasing slightly again the size of the aperture rendered the image above. In this image the seemingly blueish band has metamorphosed in more of a cyan kind of colour. The reddish area is also bigger and more vivid than before.
Image number 5. Increasing the size of the aperture, in this case has resulted in a number of substantial differences to the rendered image. First, the blueish-cyan area in the middle of the image has been replaced by a greenish-yellowish-almost-white hue. Right at the centre of the image there is a circular area that looks almost certainly white. Surrounding those two central zones is an area that could best be described as orangey. That, in turn, is enveloped by a dark reddish band. Next is a narrow circular band of a pretty much violet colour, followed by a similar band of dark blue. Lastly, a thick band of a dark green colour completes the image.
Here we have an almost complete Newtonian spectrum being created by a source of white light. I know, the conventional physicist would be quick to say that everything in this picture is easily explained by the theory of diffraction, which affirms that... I know. But I can't help thinking how flatly unimaginative the god of the conventional physicist is. I mean this god has apparently created a universe in which every single phenomenon is governed by its own distinctive set of rules, and which myriad sets of rules are more often than not clashing head-on when they're trying to develop some social bonds with each other. Nothing is simple in that universe. Everything is ridiculously complicated and devilishly cumbersome.
Take, for instance, that god's explanation of why the colours of the rainbow are running from V to R. Let me see if I can remember first what that god has decreed in that regard. Hmm... No, I can't remember exactly, and I don't care to yell "Hey Google" for such an insignificant matter. Nonetheless, I can remember that it has something to do with some turns of the spectral colours in certain media. Or something like that. The whole explanation is tedious and as stinking dubious as hell, in any event.
Compare that with what my god has done for the rainbows of my universe. The reason for the VBGYOR distribution of colours in the rainbow is a representation of their respective energy levels, which in turn are dictated by their respective spatial locations relative to the emitting source of energy. Consider a source of light, like an atom of some kind, or a star like our sun, for that matter.
Our source of energy is emitting light. The emitted light is basically colourless, but in certain areas that colourless light appears to acquire an attribute that we call colour. The colour attribute is due to the particular density of radiation at different points in space relative to the centre of the source, where the density of radiation is at its maximum and the distance between the created photons is virtually zero. At the centre of the source then the emitted light remains colourless (or white, as we call it). As the light is a disturbance in space, the light field is expanding by occupying new quanta of all the available space that's engulfing our source. So, as the disturbance of space creates ever newer photons at longer and longer distances from the centre, the created photons get 'coloured' according to the specific density of radiation at every point. Close to the central white, for example, the photons will appear V, and display the specific wavelengths and frequencies that are characteristic to that colour. A bit further away the photons will be B, then G, and so on until the last bit of visible light will be R. Once a full spectrum is completed the process starts again at the next point of expansion. See the image below.
I love what my god created in my universe, and how he governs its internal affairs. I believe in the validity of my understanding of light, for it is not only beautiful and simple. I believe in it because it has tons of advantages over the conventional understanding. Here I will give you just one concrete advantage that my understanding holds over the conventional view.
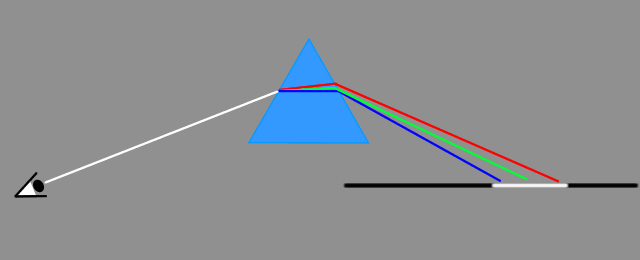
Remember Goethe's white wall controversy? At this point the conventional physicist will be quick to say that the conventional theory can fully account for that apparent anomaly, but the truth is that he's lying. The white wall issue has never been satisfactorily resolved, and if there is anyone who doesn't believe that let him come forward and argue that issue with me, in the open. I dare you, whoever you may be. Show your real colours (of course the pun is intended!) and prove that you can do more than just preach for the converted. In the meantime, I'll give you a quick demonstration of just a handful of arguments that no conventional physicist can accommodate into his badly flawed understanding.
Some of you may remember the illustration above from my past writings, or perhaps from the website of Professor Emeritus Zawisha, of Hannover University. The illustration is purportedly the full demonstration that the conventional theory can account for whatever arguments Goethe's white wall may present. To that assertion I will firstly say "Hogwash, dudes!" That I will then follow with the following.
The wall appears white because there are at least three layers of superposed colours covering it everywhere. That's according to your own theory. Tell me, then, how do the colours that you have depicted to travel backwards toward the prism know how to choose the right colour from among the three that are available at every given point? Don't say something stupid, like for example because that's how the colours are dispersed in an objective experiment.
What the hell is that white line that emerges from the prism and then enters the observer's eye? Is the colour of the wall some beam of white laser, which travels independently from one place to another? Is it that hard to understand that what the eye of the observer sees in those circumstances is an image of the prism, which carries with it an image of a white wall bordered at its apex by a B and C band and at its base by a Y and R one?
And as a last argument I will add a second prism to the illustration above. Think about this one.
Needless to say, my understanding of these issues accounts for the white wall observations without even a hint of effort. Take care.














.png)
.png)
.png)
.png)
.png)



Comments
Post a Comment